The Best Mortgage Calculator and Fun Facts Behind the Numbers

Quick and (not!) fun facts about mortgage:

• A quick dirty way to calculate your ballpark monthly payment is illustrated in the equation below. For example. If you take 1-million-dollar loan for 30-year fixed rate at 6%, then your monthly payment would be roughly 115% of one twelfth of your one year’s interest .

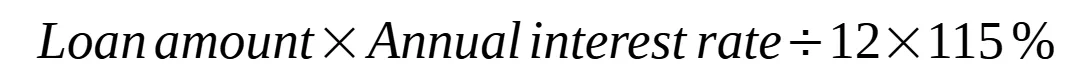
• The ratio of the interest v.s. the principal portion of your 1st monthly payment is decided by both the interest rate and the mortgage terms. For 30-year fixed rate mortgage, it’s about 6:1 with 6% rate, or
  • 8.1:1 @ 7%
  • 6.0:1 @ 6%
  • 4.5:1 @ 5%
  • 3.3:1 @ 4%
  • 2.5:1 @ 3%
  • 1:8:1 @ 2%
    Now you see how much you are burning your cash on interest when the rate is high.
• The mortgage term doesn’t affect the interest portion of your 1st month payment. A shorter mortgage term accelerates the payoff speed by bigger principal portion. The interest portion decreases (vs. a longer mortgage term) because the remaining balance becomes smaller. Thus, it helps to save your overall interest payment. A shorter-term mortgage is essentially similar to making extra principal payment.
• Your principal portion of mortgage monthly payment rises every month, but at the same rate of your (monthly) interest rate. For example, if your principal of the payment is $1,000.00, next month, it will rise to $1,005.00 assuming the rate is 6% (monthly is 6% / 12 = 0.5%)

The math behind the mortgage payment calculation.

You may wonder how the mortgage is calculated? It’s all based on three numbers: 1) your loan amount, 2) the length of the mortgage, and 3) the interest rate. And here are a few assumptions before we go deep dive into the math:

• The monthly payment is a fixed amount.
• You make the fixed amount payments till the end of the mortgage term, which is usually 30 years, or 360 payments.
• The fixed monthly amount includes two parts: the principal and the interest. The interest is calculated on an assumption that you borrow the remaining balance for one more month. The principal amount is added to make the payment amount “fixed”.
• The monthly rate is one-twelfth of the annual rate.
• Since the remaining balance reduces very month because of the principal payment, the interest decreases accordingly. The principal amount needs to be increased to keep your monthly payment unchanged.

Now let’s use M as the monthly payment; P_n is your principal portion in the n^th payment; X is the total loan amount, and r is the monthly rate (1/12 of annual rate). The equation for the 1^st month is:

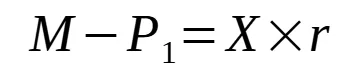
the 2^nd month is:

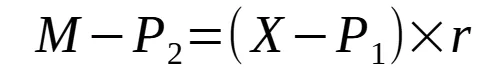
the n^th month is:

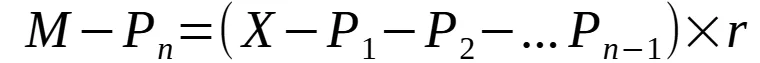
and the n+1^th month is:

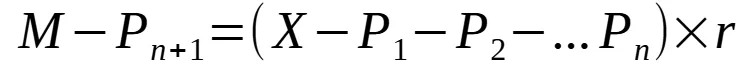
Now we subtract the n^th from n+1^th, we get:

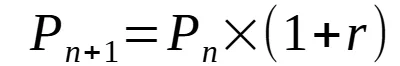
This is why the principal portion of the next month payment increase at the monthly rate. Now let’s add all the monthly principal amounts together, and the result shall equal to the total loan amount.

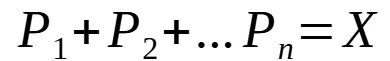
Given that the P_n is a geometric series with ratio of 1+r, the above equation can be represented as:

Let’s use the 1^st month payment equation to replace P₁, we get:

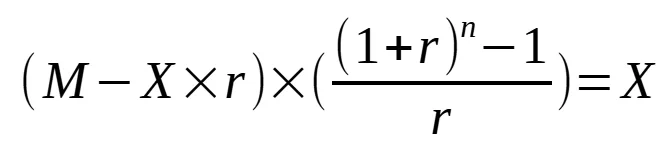
Finally, we get the monthly payment:

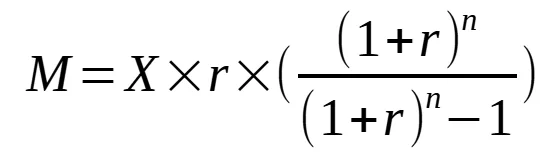
This is the equation I used to create the calculator on the top of this page.